-Limit-
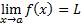
Limit Fungsi artinya nilai x mendekati nilai a (tetapi x ≠ a) maka f(x) mendekati nilai L. Sifat-Sifat Teorema Limit Fungsi Jika dan maka: , untuk Jika maka: untuk L ≠ 0 Menentukan Nilai dari Suatu Jika f(a) = k maka Jika maka Jika maka Jika atau bentuk tertentu maka sederhanakan bentuk f(x) sehingga diperoleh bentuk f(a) seperti (1), (2), dan (3). Limit Fungsi Tak Terhingga Jika pangkat tertinggi f(x) sama dengan pangkat tertinggi g(x) Jika pangkat tertinggi f(x) lebih kecil dari pangkat tertinggi g(x) Jika pangkat tertinggi f(x) lebih besar dari pangkat tertinggi g(x)
